Global InformationCovariant transformation information
 | This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages)
|
In physics, a covariant transformation is a rule that specifies how certain entities, such as vectors or tensors, change under a change of basis. The transformation that describes the new basis vectors as a linear combination of the old basis vectors is defined as a covariant transformation. Conventionally, indices identifying the basis vectors are placed as lower indices and so are all entities that transform in the same way. The inverse of a covariant transformation is a contravariant transformation. Whenever a vector should be invariant under a change of basis, that is to say it should represent the same geometrical or physical object having the same magnitude and direction as before, its components must transform according to the contravariant rule. Conventionally, indices identifying the components of a vector are placed as upper indices and so are all indices of entities that transform in the same way. The sum over pairwise matching indices of a product with the same lower and upper indices is invariant under a transformation.
A vector itself is a geometrical quantity, in principle, independent (invariant) of the chosen basis. A vector v is given, say, in components vi on a chosen basis ei. On another basis, say e′j, the same vector v has different components v′j and
The needed transformation of v is called the contravariant transformation rule.
-
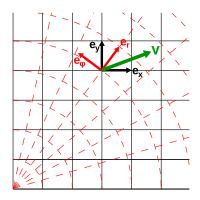A vector v, and local tangent basis vectors {ex, ey} and {er, eφ} . -
Coordinate representations of v.
In the shown example, a vector is described by two different coordinate systems: a rectangular coordinate system (the black grid), and a radial coordinate system (the red grid). Basis vectors have been chosen for both coordinate systems: ex and ey for the rectangular coordinate system, and er and eφ for the radial coordinate system. The radial basis vectors er and eφ appear rotated anticlockwise with respect to the rectangular basis vectors ex and ey. The covariant transformation, performed to the basis vectors, is thus an anticlockwise rotation, rotating from the first basis vectors to the second basis vectors.
The coordinates of v must be transformed into the new coordinate system, but the vector v itself, as a mathematical object, remains independent of the basis chosen, appearing to point in the same direction and with the same magnitude, invariant to the change of coordinates. The contravariant transformation ensures this, by compensating for the rotation between the different bases. If we view v from the context of the radial coordinate system, it appears to be rotated more clockwise from the basis vectors er and eφ. compared to how it appeared relative to the rectangular basis vectors ex and ey. Thus, the needed contravariant transformation to v in this example is a clockwise rotation.